Details
This was a reverse challenge given at DamCTF 2023. It provided a INES file that contained a NES game and a server to connect to. The server was running the game in a text interface and behaved like the provided file.
Overview
The tool that I use from now on is FCEUX, a NES emulator that also has debugging capabilities.
Opening the game we get 2 options:
- Start a new game
- Continue
Starting the game just loads the game. The challenge description had something about the player not being implemented, so we are stuck on this screen.
The continue screen requires a password to load a level. Entering an incorrect password just shows the same screen again. There is no submit button, the password is checked as soon as you enter all characters.
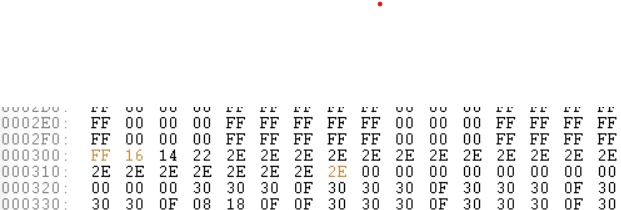
At this point I wanted to see where the input is stored in the memory. I used the Hex Editor functionallity of FCEUX to see the memory in real time. Entering and deleting characters in the password field shows that the input is stored in the memory at $302-$317. $301 appears to be the length of the input.
The input is stored as numbers between $00 and $3f. The letters are converted into numbers in the order they appear on the screed. A -> $00, B -> $01 … / -> $3f
Using the debugger, I set a breakpoint for every read in the input range. It stopped at the following sequence of instructions:
00:8273: 4A LSR
00:8274: 76 00 ROR $00,X
00:8276: B0 0D BCS $8285
00:8278: 4A LSR
00:8279: D0 F9 BNE $8274
00:827B: 88 DEY
00:827C: 30 11 BMI $828F
00:827E: B9 02 03 LDA $0302,Y @ Y is initialized with 14
00:8281: 09 40 ORA #$40
00:8283: D0 EE BNE $8273
00:8285: CA DEX
00:8286: 48 PHA
00:8287: A9 80 LDA #$80
00:8289: 95 00 STA $00,X
00:828B: 68 PLA
00:828C: 4C 78 82 JMP $8278
00:828F: EA NOP
It takes the first 6 bits of input code and concatenates the bytes in a single result in the $00-$0f range. I later realised this is basically a bse64 decoder. So far, the program just decodes the input and stores it for the next operations.
Right after the decoding loop finishes, the next code is executed
loop:
00:8290: A5 01 LDA $01
00:8292: 0A ASL
00:8293: A5 0F LDA $0F
00:8295: 2A ROL
00:8296: 49 FF EOR #$FF
00:8298: 85 0F STA $0F
00:829A: A5 0E LDA $0E
00:829C: 2A ROL
00:829D: 49 EE EOR #$EE
00:829F: 85 0E STA $0E
00:82A1: A5 0D LDA $0D
00:82A3: 2A ROL
00:82A4: 49 DD EOR #$DD
00:82A6: 85 0D STA $0D
00:82A8: A5 0C LDA $0C
00:82AA: 2A ROL
00:82AB: 49 CC EOR #$CC
00:82AD: 85 0C STA $0C
00:82AF: A5 0B LDA $0B
00:82B1: 2A ROL
00:82B2: 49 BB EOR #$BB
00:82B4: 85 0B STA $0B
00:82B6: A5 0A LDA $0A
00:82B8: 2A ROL
00:82B9: 49 AA EOR #$AA
00:82BB: 85 0A STA $0A
00:82BD: A5 09 LDA $09
00:82BF: 2A ROL
00:82C0: 49 99 EOR #$99
00:82C2: 85 09 STA $09
00:82C4: A5 08 LDA $08
00:82C6: 2A ROL
00:82C7: 49 88 EOR #$88
00:82C9: 85 08 STA $08
00:82CB: A5 07 LDA $07
00:82CD: 2A ROL
00:82CE: 49 77 EOR #$77
00:82D0: 85 07 STA $07
00:82D2: A5 06 LDA $06
00:82D4: 2A ROL
00:82D5: 49 66 EOR #$66
00:82D7: 85 06 STA $06
00:82D9: A5 05 LDA $05
00:82DB: 2A ROL
00:82DC: 49 55 EOR #$55
00:82DE: 85 05 STA $05
00:82E0: A5 04 LDA $04
00:82E2: 2A ROL
00:82E3: 49 44 EOR #$44
00:82E5: 85 04 STA $04
00:82E7: A5 03 LDA $03
00:82E9: 2A ROL
00:82EA: 49 33 EOR #$33
00:82EC: 85 03 STA $03
00:82EE: A5 02 LDA $02
00:82F0: 2A ROL
00:82F1: 49 22 EOR #$22
00:82F3: 85 02 STA $02
00:82F5: A5 01 LDA $01
00:82F7: 2A ROL
00:82F8: 49 11 EOR #$11
00:82FA: 85 01 STA $01
00:82FC: C6 00 DEC $00
00:82FE: D0 90 BNE $8290 @ loop
This code is a bit more complicated. It takes the decoded input, makes some rotations and XORs it with some constants. The constants are a sequence of numbers between $11 and $FF. The operations are executed in-place in the $01-$0f range.
The loop is executed [$00] times. This means that we can manipulate how many times this loop is executed. Setting the first byte to $00 will make the loop execute 256 time. I will later set it to $01 to make the computations easier.
Then the code adds the last 12 bytes of the input and stores them in X:A. But for each number it adds an extra 1. So in the end, the value in X:A is sum($04-$0f)+12.
The sum is then used for an integrity check. The sum has to be equal to the values stored in $01:$02. Again, this is controlled by out input.
00:8300: A9 00 LDA #$00
00:8302: A2 00 LDX #$00
00:8304: A0 0C LDY #$0C
add_loop:
00:8306: 38 SEC
00:8307: 79 03 00 ADC $0003,Y @ $0102 = #$39
00:830A: 90 01 BCC $830D
00:830C: E8 INX
00:830D: 88 DEY
00:830E: D0 F6 BNE $8306 add_loop
integrity_check:
00:8310: A4 03 LDY $03 = #$00
00:8312: 85 03 STA $03 = #$00
00:8314: 0A ASL
00:8315: A5 03 LDA $03 = #$00
00:8317: 2A ROL
00:8318: 88 DEY
00:8319: D0 F7 BNE $8312 add
00:831B: C5 01 CMP $01 = #$00
00:831D: D0 07 BNE $8326
00:831F: E4 02 CPX $02 = #$00
00:8321: D0 03 BNE $8326
00:8323: 4C A6 87 JMP $87A6 @ load_level
Right after this check, the range some of the values are copied into $0318-$0320. Putting yet another breakpoint for reads on this range showed that only the value copied from $04 is accessed. I tried setting this to $00 and it loaded the first level. Changing it to $01 loaded anoter. The description of the challenge mentioned something about the 5th level. So I tried setting it to $04 and it worked. I got the flag.
This was done editing the CPU flags while stepping through the program, so now I needed to find a way to do it from the input. I wrote a (pretty ugly) z3 script to get me an input to load the level.
Solution
from z3 import *
values = [BitVec(f"byte-{i}", 16) for i in range(16)] # 16-bit vectors to be able to add 8-bit values into a 16-biy one
values2 = [BitVec(f"byte2-{i}", 16) for i in range(16)]
su = BitVec("sum", 16)
s = Solver()
for i in range(16):
s.add(values[i] >= 0)
s.add(values[i] <= 0xff)
s.add(values2[i] >= 0)
s.add(values2[i] <= 0xff)
s.add(values[15] & 0x7 == 0) # Not sure why, but the last 6 bits seem to be always 0
s.add(values[0] == 1)
# One iteration ($00 = 1)
s.add(values2[0xf] == (((values[0x01] >> 7) + (values[0xf] << 1)) ^ 0xff) & 0xff)
s.add(values2[0xe] == (((values[0x0f] >> 7) + (values[0xe] << 1)) ^ 0xee) & 0xff)
s.add(values2[0xd] == (((values[0x0e] >> 7) + (values[0xd] << 1)) ^ 0xdd) & 0xff)
s.add(values2[0xc] == (((values[0x0d] >> 7) + (values[0xc] << 1)) ^ 0xcc) & 0xff)
s.add(values2[0xb] == (((values[0x0c] >> 7) + (values[0xb] << 1)) ^ 0xbb) & 0xff)
s.add(values2[0xa] == (((values[0x0b] >> 7) + (values[0xa] << 1)) ^ 0xaa) & 0xff)
s.add(values2[0x9] == (((values[0x0a] >> 7) + (values[0x9] << 1)) ^ 0x99) & 0xff)
s.add(values2[0x8] == (((values[0x09] >> 7) + (values[0x8] << 1)) ^ 0x88) & 0xff)
s.add(values2[0x7] == (((values[0x08] >> 7) + (values[0x7] << 1)) ^ 0x77) & 0xff)
s.add(values2[0x6] == (((values[0x07] >> 7) + (values[0x6] << 1)) ^ 0x66) & 0xff)
s.add(values2[0x5] == (((values[0x06] >> 7) + (values[0x5] << 1)) ^ 0x55) & 0xff)
s.add(values2[0x4] == (((values[0x05] >> 7) + (values[0x4] << 1)) ^ 0x44) & 0xff)
s.add(values2[0x3] == (((values[0x04] >> 7) + (values[0x3] << 1)) ^ 0x33) & 0xff)
s.add(values2[0x2] == (((values[0x03] >> 7) + (values[0x2] << 1)) ^ 0x22) & 0xff)
s.add(values2[0x1] == (((values[0x02] >> 7) + (values[0x1] << 1)) ^ 0x11) & 0xff)
s.add(values2[0x3] == 1)
s.add(su == values2[0x4] + values2[0x5] + values2[0x6] + values2[0x7] + values2[0x8] + values2[0x9] + values2[0xa] + values2[0xb] + values2[0xc] + values2[0xd] + values2[0xe] + values2[0xf] + 12)
s.add(values2[0x1] == ((su << 1) | ((su&0xff) >> 7)) & 0xff)
s.add(values2[0x2] == su >> 8)
s.add(values2[0x4] == 0x4)
print(s.check())
m = s.model()
alphabet = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/"
# This is just base64 encode
bn = ""
for i in range(16):
val = m[values[i]].as_long()
bn += f"{val:08b}"
bb = [int(bn[i:i+6],2) for i in range(0,len(bn), 6)]
print("".join([alphabet[x] for x in bb])) # AQ+UGSBUSEQygwqCGREIgA
Other resources: https://www.nesdev.org/
